Основная идея этой главы – рассмотреть концепт «наглядность» с философской точки зрения. Я попытаюсь показать, что в том его понимании, которое здесь представлено, он сможет стать надежным критерием суждений о правильности (или неправильности) наших теоретических построений. В общем-то, я утверждаю то, что давно интуитивно принято и постоянно используется. Но когда вы захотите опереться на существующие взгляды на наглядность, то очень скоро выясните, что она была незаслуженно отнесена к таким категориям, которые как бы изначально понятны и не требуют никаких дополнительных пояснений. На самом деле, как мы увидим ниже, это совсем не так. Отсутствие подробных объяснений основных характеристик концепта наглядности существенно ограничивает наши возможности воспользоваться им в полном и незамутненном виде. Словом, мне кажется, что требуется подробная и тщательная формулировка главных качеств и особенностей наглядности, что и является целью настоящей главы.

Огл.  Существующий взгляд на наглядность

Ссылку на данный концепт можно встретить в десятках тысяч публикуемых работ, и везде он утверждается как нечто настолько очевидное и убедительное, что понимается и принимается без предъявления дальнейших доказательств. Это нечто либо сразу превращается в достоверность, либо оно уже, якобы, было проанализировано ранее и доведено до такой степени осмысления, которое может считаться окончательным и не требующим дальнейших подтверждений.

Основанием для такого рода убежденности является тот факт, что наглядность изначально опирается на свидетельства нашего зрения. Мы видим – значит, мы постигаем. Мы видим – значит, мы легко ориентируемся в окружающей действительности и можем использовать это обстоятельство для воплощения наших планов в онтологической реальности. «Лучше один раз увидеть, чем сто раз услышать», – гласит народная мудрость.

При этом нельзя забывать, что видим мы с помощью глаз, но расшифровываем увиденное и понимаем его значение с помощью мозга. Глаза выступают лишь в роли проводника, доносящего картинку до мозга, где она фиксируется и подвергается анализу. Навыки адекватной расшифровки увиденного тренируются с детства и становятся со временем все более изощренными и зрелыми. У людей, по какой-либо причине лишенных в детстве зрения и восстановивших его после значительного промежутка времени, наступает пора привыкания к правильной трактовке того, что они увидели. Это – мучительный процесс, продолжающийся иногда годами и не всегда достигающий нужных результатов. Поэтому родители и школа обязаны не только поставлять взыскующему детскому уму различные познавательные ситуации, но и помогать им в их правильной расшифровке. По-видимому, это – главная функция обучения детей, да и взрослых.

Убедившись, что опора на увиденное помогает справляться с насущными заботами, люди на протяжении всей истории старались улучшить возможность наглядного постижения реального мира вокруг и внутри себя. Они придумывали всевозможные приспособления, чтобы видеть больше и лучше. Для этого они изобрели очки, бинокли, микроскопы, телескопы, перископы и даже такие приборы, которые позволяют увидеть невидимое. Так, невозможно увидеть с какой скоростью мы шагаем, но с помощью шагомера проблема эта решается, и на приборе мы видим скорость собственного передвижения. А с помощью спидометра можно определить скорость движения автомашины.

Невозможно невооруженным глазом увидеть атомы и атомные частицы в синхрофазотроне, но если поместить в него экран, то по следам ударов разогнавшихся частиц можно судить о них самих и скорости их передвижения. Возникает, так сказать, «опосредованная» наглядность, которая затем переводится в реальные представления материального характера. Это – уже знаковая наглядность, временно подменяющая хорошо нам знакомую наглядность онтологического плана. Существуют знаки, которые специально приспособлены для фиксации подобной наглядности и для последующего ее перевода в наглядность «подлинную», то есть непосредственную.

Именно так слово наглядность отражается в различных языках. Абсолютно прозрачна этимология этого слова в русском: оно происходит от слова «глядеть». По-английски ему соответствует visuality, восходящее к латинскому vedere, опять же со значением «видеть, увидеть». В немецком anschaulich (наглядный) явно соотносится с schauen (смотреть, вглядываться). Наиболее распространен этот термин в педагогике, там под наглядностью разумеется такое свойство изучаемого материала, которое позволяет его увидеть в доступном для понимания и запоминания виде. И, опять-таки, либо в прямом его реальном воплощении (картинки, макеты, фильмы), либо в опосредованном виде (торричеллиеву пустоту нельзя увидеть, но в ходе демонстрируемого опыта она адекватно воспринимается нашим сознанием).

Очень странно, что концепт наглядности не был подвергнут тщательному философскому рассмотрению. Мне не известно ни одного крупного труда по наглядности, а в специальных областях знания я знаю лишь одну докторскую диссертацию В. П. Бранского^[45]. Собственно говоря, именно эта работа и побудила меня заняться вплотную данной проблемой. Автор диссертации утверждает, что в физике наглядность как таковая исчезает и «...принцип наглядности заменяется принципом ненаглядности». С этим я никак не могу согласиться. В действительности, по-моему, принцип наглядности просто видоизменяется по форме, но во всех случаях остается неистребимым по существу. Этот тезис я и буду неизменно доказывать в последующем изложении.

Мой анализ понятия наглядности будет строиться на трех основных утверждениях:

а) наглядность даже в самых абстрактных и отдаленных от повседневной реальности размышлениях не исчезает – она лишь дистанцируется от обычного понимания того, что непосредственно воспринимается нашим зрением и другими органами чувств;

б) если в ходе познания прямая наглядность исчезает, то она частично подменяется знаковой наглядностью;

в) выводы, полученные в рассуждениях с использованием абстрактной наглядности, не могут считаться окончательными до тех пор, пока мы не продемонстрируем их в терминах наглядности обычной.

Огл.  Распространение понятия наглядности на показания иных рецепторов

Первое отступление от первоначального представления о наглядности происходит тогда, когда мы убеждаемся, что наглядно не только то, что мы видим, но и любое непосредственное ощущение организма. Из них самым ранним является реакция новорожденного на материнское молоко, которое он высасывает еще с закрытыми глазами. Однако очень скоро именно зрительное восприятие начинает играть главную роль среди всех сенсорных систем, коими мы наделены от природы. Это относится, прежде всего, к так называемым органам чувств, которые обслуживают зрение, слух, обоняние, вкусовые и тактильные ощущения (т. е. осязание), но не только к ним. Мы в немалой степени зависим от мышечной координации и от прочих организующих наше поведение функций организма, которые обеспечивают нашу взаимосвязь с окружающей средой. Существует подсчет, согласно которому зрение предоставляет нам от 80 до 90% всей информации по поводу внешней среды.

Кроме того, у нас есть еще и внутренние показатели самочувствия, которые тоже весьма наглядны: боль нами ощущается как серьезное недомогание, жар – как признак наступающей болезни и т. д. Так же, как и в случаях с внешними раздражителями, они заставляют нас реагировать и предпринимать шаги по устранению неполадок.

Создание приборов, помогающих врачам распознавать заболевания, получило особое развитие за последние сто с небольшим лет, после того как стало понятно, что открытие Вильгельма Конрада Рентгена может быть использовано в медицине. Целью всей инструментальной диагностики – рентгенографии, ультразвукового исследования, компьютерной томографии – является усиление наглядности. Надо заметить, что к этому же стремилась и прежняя медицина, использовавшая методы физикальной (использующей только собственные органы чувств) диагностики, – пальпацию, аускультацию и перкуссию.

Очень скоро по молчаливому согласию люди стали понимать под наглядностью все естественные и искусственно усиленные способы получения «чувственного» восприятия информации. С точки зрения (весьма характерное для нашей темы выражение^[46]) человека, получающего такую информацию, любое подобное восприятие оказывается достаточно наглядным для принятия соответствующих практических решений. Все же остальные случаи наглядности мы, в конечном счете, вынуждены сводить к наглядности данного вида, прежде чем строить на их основе какое-либо решение. Об этом и пойдет речь в последующих разделах.

Огл.  Переход на знаковую наглядность

Указанная выше наглядность возможна, однако, только для ограниченного числа познавательных ситуаций. Она работает лишь в обстоятельствах непосредственного контакта с изучаемым событием либо с его очень конкретным представлением. По семиотической терминологии – только тогда, когда мы имеем дело с естественными знаками и с нижним регистром образных знаков. Естественные знаки свидетельствуют о скрытой для глаза цельной картине, которая восстанавливается человеком исходя из его прежнего опыта (скажем, когда, выходя из дома, он видит дождевые облака и поэтому берет с собой зонтик). А нижний регистр образных знаков включает в себя рисунки, фотографии и их производные, по которым тоже можно судить о познаваемой ситуации (человек берет с собой зонтик и тогда, когда о дожде говорится в сводке погоды). На более высоком уровне образных знаков непосредственная наглядность уже невозможна (так, нельзя сделать никаких практических выводов из абстрактной живописи).

В этом случае мы вынуждены отказаться от непосредственной наглядности и обращаемся к наглядности таких знаков, которые лишь косвенно и опосредованно свидетельствуют о каких-то чертах изучаемого процесса. При этом и подбор знаков, и их трансформация начинают зависеть как от онтологических законов изучаемых явлений, так и, не в меньшей мере, от правил знаковой системы, в которую данные знаки включены. Получается как бы двойная подчиненность гносеологической ситуации – как онтологической реальности, так и семиотической, – и обе должны нами учитываться, если мы хотим прийти к правильным выводам. Оба вида зависимости отражаются в метаязыке используемой знаковой системы, который предписывает правила работы с ней. В мою задачу не входит подробно разбираться в данном вопросе. Я хочу только показать, как от системы к системе, по мере повышения абстрактности входящих в них знаков, все больше исчезает первичный тип наглядности, а также изменяется характер проявляющейся в них знаковой наглядности. Ниже я остановлюсь на нескольких видах знаковой наглядности в последовательной цепочке ее метаморфоз по этому параметру в различных системах знаков.

Огл.  Первый этап знаковой наглядности

Знаковая наглядность изменяется в указанном направлении: чем выше абстрактность используемых нами знаков, тем больше наглядность дистанцируется от своей первоначальной привязки к чувственному восприятию и начинает зависеть от формы и содержания знаков. Поскольку исследуемые здесь этапы наглядности становятся все более абстрактными, это затрудняет их понимание и последующую апробацию в онтологии, вне знакового мира. Последнее замечание очень важно для дальнейших рассуждений. Знаковая наглядность, по-моему, всегда остается связанной с первичным видом наглядности. Но именно потому, что в знаковом исполнении она зачастую не может быть нами увидена и принята до конца, она требует для себя последующего подтверждения в эксперименте. Поэтому в каждом случае ее трансформаций я буду также говорить и о возможностях подтвердить выводы знаковой реальности в онтологической реальности. Так что переход к знаковой наглядности вовсе не означает полный отказ от ее первоначального наполнения и согласие с принципом ненаглядности. Наоборот, наглядность знаков имманентно привязана к наглядности чувственной.

Первые образцы знаковой наглядности всегда опираются на наш чувственный опыт. Возьмем самый простой пример: дробь 256/512 значительно менее наглядна, чем 1/2. Поэтому, если мы получили в результате вычислений первую дробь, мы ее сокращаем до 1/2. Почему же половинка так наглядна? Да потому, что она опирается на наш повседневный опыт, и потому, что в мозгу легко возникает образ предметов, разделенных пополам. Таких чувственно воспринимаемых знаков достаточно много, и мы постоянно опираемся на них в своих рассуждениях. Если знаки оказываются «ненаглядными», им на помощь приходят другие знаки. Так, дробь показанная выше (256/512), – ненаглядна, но становится наглядной после сокращения.

Есть и другие способы: один из них – использование знаков меньшей степени абстрактности. Обратите внимание, как в русском языке слова объясняют соответствующие им дроби. До дроби 1/5 все предыдущие аналогичные дроби можно заменить их словесными эквивалентами (1/2 – «половинка», 1/3 – «треть», 1/4 – «четвертинка»). Затем вступает в силу сочетание со словом «часть»: «пятая часть от…», «шестая часть от…» и т.д. Когда дробь достигает запредельных высот (после первой сотни), мы отказываемся от замены и просто называем число (1/102 «одна сто-вторая» и пр.). Так словесные синонимы постепенно достигают предела, за которым они уже становятся «ненаглядными» и поэтому бессмысленными. Остаются только действия с соответствующими числами.

Замена «ненаглядных» знаков «наглядными» происходит во многих познавательных ситуациях. При объяснении слов в словаре мы к словесным определениям часто добавляем рисунки. Литературные тексты сопровождаются иллюстрациями, а формулировки физических законов – опытами, которые делают понятными чисто словесные пояснения. И везде это происходит по принципу: более абстрактные знаки подкрепляются менее абстрактными.

Все простые рисуночные представления действительности – рисунок расположения предметов на местности либо просто предмета в качестве иллюстрации к словарной статье – относятся к такого рода знакам. Именно поэтому мы так часто прибегаем к рисункам и простым графическим схемам в своих объяснениях. Скажем, при объяснении состава того или иного вещества мы охотно рисуем составляющие его атомы. Например, молекулу воды мы можем представить так:

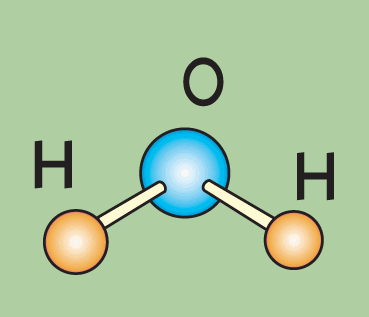
Естественно, что это значительно наглядней химической формулы Н₂О. Более сложными для понимания являются схемы, допустим, чертежи тех или иных весьма абстрактных явлений, но и они, так сказать, «овеществляют» сухие теоретические выкладки. Вы никогда не задумывались над вопросом, почему вся геометрия «положена» на чертежи? Во-первых, потому, что она касается пространственных отношений, легко представимых в чертежах; а, во-вторых, потому, что они наглядно иллюстрируют все наши математические выкладки об этих самых отношениях (ведь мы могли бы не обращаться к чертежам, ограничившись словесными объяснениями).

Не случайно на заре человеческой цивилизации люди в своих объяснениях окружающей действительности обращались к знакам, которые совершенно нагляд-но объясняли происходящее. Яркий пример – теория древних греков о строении Вселенной, которая сопровождалась наглядной схемой, – изображением нескольких сфер, вращающихся вокруг Земли. В каждую сферу были включены яркие звезды, видимые на небосклоне и уже известные грекам. В начале истории объяснение явлений действительности происходило на основе мало абстрактных и наглядных с точки зрения наших предков знаков.

Обратимся к еще одному конкретному примеру – определению длины окружности. В Вавилоне эта проблема решалась путем включения круга в квадраты – внешний и внутренний по отношению к кругу. Средняя величина между их периметрами считалась длиной окружности и вполне адекватно применялась на практике. Понятно, что этот результат был очень неточным, и людям пришлось уточнять его, совершенствуя первоначальный метод. Вот как это выглядит на рисунке:

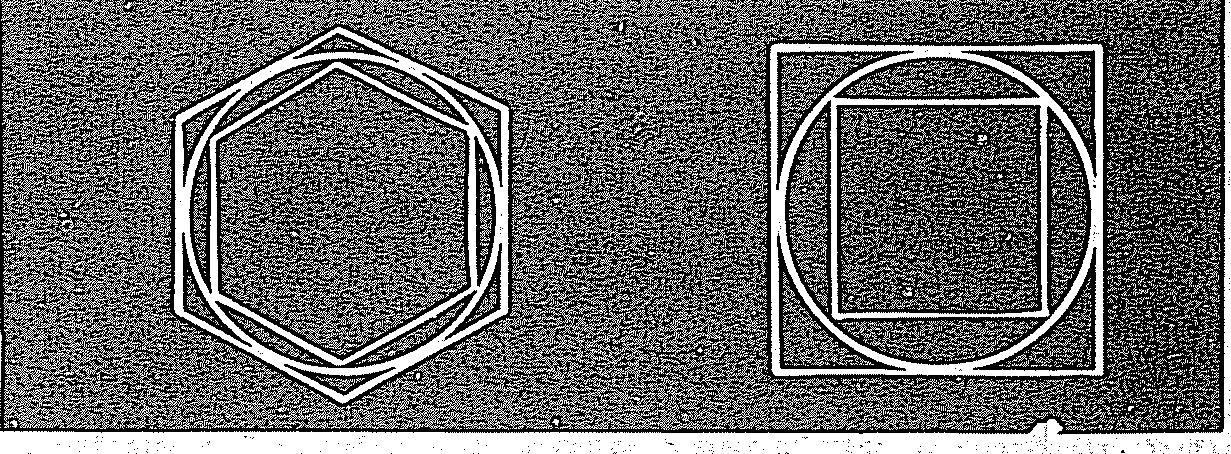
На левом чертеже представлена усовершенствованная версия определения длины окружности – с использованием правильных многоугольников, которые, естественно, ближе к окружности своими сторонами. Эту процедуру можно было повторять снова и снова, каждый раз увеличивая число сторон многоугольника и приближаясь к все более точному итогу. Данный метод был хорош для получения = приблизительных результатов, но не годился для более точных расчетов. Таковые удалось получить, лишь обратившись к внутренним ресурсам круга как геометрической фигуры, но для этого требовался научный подход и обращение к более абстрактным знакам. Это стало возможным на следующем этапе использования знаковой наглядности.

Огл.  Знаковая наглядность в развитой науке

Следующий этап знаковой наглядности связан с тем, что каждое научное направление стало строить свою парадигму, где отчетливо просматривался собственный тип знаков и только этой парадигме присущая стратегия их обработки. Химия имеет свою систему знаков, для которой разработаны специальные алгоритмы манипулирования с ними (точнее, для каждого раздела химии в этом деле существует своя специфика). То же самое происходит в физике, лингвистике и в любой другой науке. Не будет преувеличением сказать, что именно с этого момента и возникает зрелое научное знание. До этого тоже происходила деятельность специфически химического характера, но она еще не оформилась в зрелую науку. Так, до получения своей системы знаков неорганическая химия оформлялась несколько тысячелетий, но только после того, как устоялись постоянные и общепринятые знаки и правила обработки каждого из них, она превратилась в зрелую научную отрасль знаний.

Пока в медицине основными методами борьбы с недомоганиями оставались молитвы и принесение даров богам и святым, трудно было говорить о ней как о науке. Лишь когда врачи научились исследовать возникновение и ход болезней и воздействовать на реальные причины заболеваний, можно было заявить о ней как о зрелой науке. Тогда медицина стала приобретать опыт самостоятельности и умение обращаться к причинам и следствиям в одном ключе. Пока в разных странах единицей измерения служили части тела (локоть, ступня – английский фут), невозможно было научно подойти к мерам длины. Только после определения метра как всеобщей меры длины стала возможной наука об измерениях – метрология. А от него (метра) и в сравнении с ним пошли уже и остальные меры, больше и меньше метра, превратившись в единую стандартизированную систему измерения длины.

Опора на собственные силы в конкретной знаковой и научной системе определяет статус любого гносеологического направления: только после того, как оно согласовывает специфический предмет и методы изучения и выражает их в непохожих на другие системах знаков, данное направление можно считать подлинно научным и самостоятельным. Картография стала наукой только после того, как поместила изображение земной поверхности в сетку параллелей и меридианов, разработала свои собственные условные обозначения и определила математические модели для переноса изображений на глобусы и двумерные карты. До этого она ограничивалась случайными рисунками, схемами отдельных территорий и произвольными наборами знаков, и поэтому наукой еще не была. Математические изыскания пронизывают историю любой цивилизации, но они оформились в науку только после их сведения в несколько связанных между собой систем знаков, обрабатываемых по определенным, заранее установленным для них алгоритмам.

Данное свойство кристаллизации систем знания в конкретные отрасли науки сопровождается необходимостью представить возникающие системы знаков в наиболее убедительной, то есть наиболее наглядной форме. При этом проявляется весьма парадоксальное свойство этих систем: оказывается, что вовсе не обязательно выяснять до конца их онтологическую природу, достаточно выделить какую-то общую их характеристику и точно определить параметры ее проявления и метаморфоз. Скажем, мы изучаем химические элементы. Мы можем сосредоточиться на выяснении того, что это такое, как и почему тот или иной элемент возник, а можем изучать любой элемент как данность на текущий момент времени. Тут я повторяю тезис де Соссюра о возможности синхронного и диахронного изучения языков. Можно изучать язык с точки зрения того, как и когда он появился и как развивался (диахронная позиция), а можно сосредоточиться на его состоянии в данный момент времени (синхронная позиция). Действительно, существует два подхода к изучению языков. В конечном счете они комплементарны (дополняют друг друга), но по преимуществу используются раздельно.

Я хотел бы распространить этот тезис на любую науку, а не только на лингвистику. В любой науке мы можем сосредоточиться на истории ее возникновения и усилиях предстать в виде законченной и цельной системы, а можем заняться выяснением характеристик ее конкретных и уже известных проявлений. В конечных выводах оба эти подхода сливаются в единый конкретный результат, который оказывается наиболее наглядным для данной науки. В физике, например, он появляется в виде формул. Вовсе не обязательно, хотя и желательно из дидактических соображений, изучать, как появилась та или иная формула. Достаточно понять ее содержание и поупражняться в ее применении. После этого можно, не задумываясь, использовать ее для практических расчетов. Если я знаю формулу расчета силы тока, то я ее и применяю на практике, даже не усвоив истории ее появления. Как справедливо замечено, «можно начертить прямую линию, не задумываясь о том, что она состоит из точек».

Именно формулы являются проявлением наглядности в физике, равно как и в алгебре и тригонометрии. В химии эту же функцию выполняют записи разных видов реакций. Фактически, так происходит изучение большинства дисциплин в школе: дается формула, кратко объясняются ее составляющие, и происходит тренировка в ее практических приложениях. Важно только показать, что данная формула работает на практике, что ее результаты применимы. Ее перенос в онтологическую практику – необходимое условие утверждения знаковой реальности в человеческом сознании. В геометрии, где изучаются пространственные фигуры, утверждение наглядности происходит иным способом – через начертание дополнительных построений, доказывающих правильность выводимых при этом результатов. Вот почему основой изучения этой науки являются теоремы и словесное разъяснение их наглядных построений. Но и в геометрии требуется показать, что конечный вывод теоремы приемлем на практике, – иначе он не станет для нас наглядным.

Сравнение двух образцов знаковой реальности (в алгебре и геометрии) оказывает, насколько разнообразны способы выражения наглядности в гносеологических ситуациях с использованием абстрактных знаков. Геометрия гораздо ближе к онтологической реальности, чем алгебра. Она оформилась как наука на две тысячи лет раньше, а ее знаки значительно менее абстрактны. Поэтому в геометрии возможны совсем иные способы достижения наглядности, нежели в алгебре, где остаются лишь доказательства наглядности ее формул в их практическом применении. Еще дальше отстоит наглядность в ее интуитивном понимании от знаковых манипуляций в логике. Там даже практические выводы не всегда убедительны. Поэтому в логике пришлось прибегнуть к чисто формальным способам утверждения наглядности, не выходящим за пределы самих логических схем, – так называемым «таблицам истинности», которые чисто технически удостоверяют, что все знаковые трансформации выполнены правильно. Они по определению никак не совпадают с критерием практической проверки ложности либо истинности полученных выводов.

Зато в естественных науках такого рода проверка считается обязательной. Какой бы сложной и абстрактной ни казалась проблема, ее окончательное разрешение должно быть проверено на практике для удостоверения того, что оно правильно. В этом случае способом проверки является эксперимент, поставленный в абсолютно наглядном режиме. Именно поэтому результаты естественных наук признаются более достоверными, нежели чисто теоретические утверждения, основанные только на логике изложения. Удостоверение теоретических выкладок Эйнштейна по поводу строения Вселенной было отложено до 1919 года, хотя сама теория в ее первоначальном виде была сформулирована еще в 1905-м, а соображения об искривлении света под влиянием притяжения Солнца – в 1915 году. Человечеству пришлось дождаться затмения Солнца, когда оно было закрыто Луной, чтобы измерить отклонение лучей, предсказанное Эйнштейном; лучей, проходивших рядом с Солнцем, но не видимых в его свете. Учение о черных дырах было сформулировано в 60-х годах прошлого века, но свое первое подтверждение на практике оно получило лишь в феврале 2014 года, когда были зафиксированы выбросы излучения, происходившие от взрыва исчезнувшей черной дыры.

Все эти и подобные им примеры убеждают нас в том, что наглядность в знаках существует и что она связана с реальной наглядностью, которая в конечном итоге либо ее принимает, либо отвергает.

Огл.  Опора на подобные и метафорические знаки в программировании

Любопытный материал о зависимости наших самых абстрактных выкладок от опоры на уже известные когнитивные структуры предоставляет нам сегодняшняя практика создания информационных технологий. Дело это совершенно новое, и большинство из создаваемых компьютерных технологий не имеет аналогов и прецедентов, на которые могли бы опереться их создатели. Им приходится ориентироваться только на условия той задачи, которая перед ними ставится, оценивать ее практические реквизиты и придумывать решения в виде всевозможных метафорических предтеч своих будущих творений. Они представляют себе конкретные параметры возможных продуктов и мысленно опираются на их метафорическую (виртуальную) модель, которая позволяет им создать возможный образ будущего продукта. Метафорическая модель позволяет им наметить параметры и последовательность работы по изготовлению нужного продукта. Это, разумеется, не единственный способ изобретения необходимых сегодня информационных технологий, но, во всяком случае, один из магистральных путей их создания.

В моем представлении это также обращение к наглядности, наглядности непрямой и далеко отстоящей от тех первичных средств ее выражения, которые были описаны выше. Таким образом, в связи с увеличением в знаках степени абстрактности, нам приходится искать поддержку в наглядности знаковой, хотя она иногда очень далека от идеала. Полный отказ от наглядности – онтологически либо семиотически обоснованной – привел бы к потере ориентиров в ходе познавательной деятельности человека. И здесь я абсолютно солидарен с Норбертом Винером, одним из создателей кибернетики, который писал: «Кстати, я убежден, что если существует какое-то одно качество, которое отличает действительно талантливого математика от его менее способных коллег, то оно состоит в умении оперировать врéменными, только ему понятными символами, позволяющими выражать возникающие у него идеи на некоем условном языке, который нужен лишь на определенный отрезок времени. Если математик не обладает этим умением, он никогда ничего не достигнет, так как сохранить мысль в несформулированном виде абсолютно невозможно. (Курсив мой. – А.С.)»^[47]

Следует отметить, что обращение к метафорическим моделям есть обращение к знаковой реальности, которая действует на время создания продукта, но непременно проверяется потом в его практической пригодности и эффективности. Именно такая онтологическая проверка в конечном итоге наглядно удостоверяет качество нового изделия.

Огл.  Избавление от излишней абстрактности как способ достижения наглядности

Отмеченный выше метод обращения к знаковой наглядности с использованием врéменных знаков – эффективен лишь в период создания новых идей и интеллектуальных продуктов, = когда ученому предоставляется право опираться на временные, переменные и лично ему принадлежащие знаковые конструкты. Ситуация коренным образом меняется, когда работа над новым продуктом заканчивается. Возникает необходимость объяснить принципы создания и содержание разработок = другим людям, а для этого ученый должен использовать уже существующие и конвенционально одобренные знаки, иначе его просто не поймут. Разумеется, он может предложить новые знаковые построения, но и в этом случае он манипулирует принятыми ранее понятиями и концептами. Делается это обычно в виде языковых сообщений – язык как знаковая система приспособлен для объяснения всех знаковых комбинаций (новых и старых), произведенных в любой семиотической системе. Другими словами, знак любой семиотической природы всегда получает вербальное дублирование.

Находясь по моей схеме в середине знакового континуума, на равном расстоянии от наиболее и наименее абстрактных знаковых схем, язык получает возможность комментировать любую из них. Язык пронизывает всю нашу когнитивную активность и со временем становится толмачом всех наших начинаний – и теоретических, и практических. Поэтому, придя к новому, еще не известному для других результату, мы обращаемся именно к языку за объяснением происходящего. Язык располагает возможностями вербализации любого интеллектуального продукта; в нем имеются ресурсы для объяснения новых вещей как специалистам, так и самым неподготовленным «чайникам».

Язык позволяет выбирать словесные средства разной степени абстрактности, доступные каждому из нас (речь, разумеется, не идет об олигофренах). Если возникает необходимость, то словесные пояснения сопровождаются знаками из неречевых систем (рисунки, схемы, диаграммы и пр.).

Пользуясь языковыми ресурсами, всегда можно объяснить суть новых разработок, прибегнув при этом к уже известным твоему собеседнику концептам. Они делают объяснения наглядными, а, следовательно, и понятными. В наших объяснениях должны обязательно присутствовать и предлагаемые авторами новых открытий способы их практического приложения, то есть перенос их в онтологическую плоскость в виде возможных реальных аппликаций.

Огл.  Наглядность для укрепления знаковых систем

Существует дополнительный вид знаковой наглядности, еще дальше отстоящий от «прямой» наглядности, чем представленные выше примеры. Впрочем, он еще более «знаковый», чем те, которые обозначены в предыдущих разделах, потому что замыкается на знаковой реальности и лишь потом, иной раз в далеком будущем, удостаивается эмпирического подтверждения. Он связан с усовершенствованием существующих знаковых систем и с созданием новых систем знаков. Я отношусь к знакам и их системам как к орудиям нашего умственного труда. Подобно другим орудиям (скажем, молотку или лопате), знаки постоянно совершенствуются и приобретают дополнительные качества и свойства. Но, в отличие от молотка либо лопаты, их полезность и даже необходимость самого их существования, совсем не очевидны. Они зачастую проявляются лишь через весьма продолжительное время, в течение которого новые варианты знаков остаются в подвешенном состоянии и подвергаются непрестанным нападкам со стороны оппонентов.

Такого рода препятствия на пути новых теорий в математике стали называть кризисами математической мысли, и их насчитывается, по крайней мере, три на протяжении известной нам истории этой науки. Первый из них был связан с изобретением комбинированных чисел, второй – с появлением мнимых чисел, а третий – с теорией множеств, разработанной Георгом Кантором на пороге XIX столетия. Я остановлюсь на последнем случае, поскольку он ближе к нам по времени и хорошо документирован.

Позволю себе привести длинную цитату об этом кризисе из Википедии, поскольку она кажется мне достаточно понятной и исчерпывающе объясняющей суть дела: «Георг Кантор ˂…˃ – немецкий математик. Он наиболее известен как создатель теории множеств, ставшей краеугольным камнем в математике. Кантор ввел понятие взаимно-однозначного соответствия между элементами множеств, дал определение бесконечного и вполне-упорядоченного множеств и доказал, что действительных чисел „больше“, чем натуральных. Теорема Кантора фактически утверждает существование „бесконечности бесконечностей“. Он определил понятия кардинальных и порядковых чисел и их арифметику. Его работа представляет большой философский интерес, о чем и сам Кантор прекрасно знал.

Теория Кантора о трансфинитных числах первоначально была воспринята настолько нелогичной, парадоксальной и даже шокирующей, что натолкнулась на резкую критику со стороны математиков-современников, в частности, Леопольда Кронекера и Анри Пуанкаре, позднее – Германа Вейля и Лёйтзена Эгберта Яна Брауэра, а Людвиг Витгенштейн высказал возражения философского плана. Некоторые христианские богословы увидели в работе Кантора вызов уникальности абсолютной бесконечности природы Бога, приравняв однажды теорию трансфинитных чисел к пантеизму. Критика его трудов была порой очень агрессивна: так, Пуанкаре называл его идеи „тяжелой болезнью“, поражающей математическую науку; а в публичных заявлениях и личных выпадах Кронекера в адрес Кантора мелькали иногда такие эпитеты, как „научный шарлатан“, „отступник“ и „развратитель молодежи“. Десятилетия спустя после смерти Кантора Витгенштейн с горечью отмечал, что математика „истоптана вдоль и поперек разрушительными идиомами теории множеств“, которые он отклоняет как „шутовство cмехотворное и ошибочное“»^[48].

К настоящему времени вся эта критика сошла на нет. Теория Кантора стала основой многих разделов математики – общей топологии, общей алгебры, функционального анализа – и оказала существенное влияние на современное понимание предмета математики вообще. Суть преодоленного математического кризиса заключается в том, что новые знаковые разработки никак не могут отвергаться с порога на том основании, что они непонятны, ненаглядны и не в состоянии поэтому служить продолжением принятым сегодня воззрениям. Приходится долго ждать, пока практические жизненные интересы не вынесут по этому поводу свой окончательный вердикт. В конечном счете именно это обстоятельство оказывается решающим.

В период же ожидания нам приходится довольствоваться косвенными критериями пригодности или непригодности предложенных нововведений. К ним относятся, прежде всего, признаки «вписываемости» новых знаковых образований в старый и апробированный корпус знаний соответствующей области знаний, как-то: полнота системы, закрывает ли предложенный материал лакуны в этом корпусе, ведется ли разговор на соответствующем языке и другие подобные соображения. Существует также критерий некоей гармоничности представляемых результатов и даже их эстетического наполнения. Словом, нам приходится опираться на некоторые формально не завершенные доказательства, но тут уже ничего не поделаешь – в нашей жизни многое покоится на неокончательных суждениях. Например, в судебной практике часто приходится выносить весьма суровые приговоры на основе косвенных, а не прямых улик. Этот юридический принцип принимается как некоторое необходимое условие – не оставлять преступление безнаказанным. Все отлично понимают, что он может привести к ошибочному осуждению. Поэтому заранее учреждаются некоторые корректирующие процедуры: множество высших инстанций, имеющих право отменить приговор, пересмотреть дело по вновь открывшимся обстоятельствам и пр. Точно так же и в нашем случае за эмпирикой и жизненной практикой остается право вынести по спорному делу о наглядности того или иного предмета свой окончательный вердикт, несмотря на срок давности конкретной проблемы.

Огл.  Ошибки прямой наглядности

Вот, пожалуй, и все, что я хотел сказать о наглядности. Остается написать несколько слов об опасности высказываний людей, которые чересчур доверяют своим ощущениям по поводу вещей, подлежащих обсуждению с разных точек зрения. Наглядность не только является неотъемлемой частью любого познавательного процесса; она еще часто оказывается причиной ошибок в наших поспешных суждениях. Непродуманное и самоуверенное убеждение в собственной правоте, основанное на показаниях органов чувств, часто ведет к ошибочным мнениям.

Иногда такие мнения продолжают жить многие столетия, как это произошло с космологией Птолемея, поставившей Землю в центр мироздания, а Солнце и все прочие небесные тела полагавшей вращающимися вокруг Земли. Теория Коперника опровергла эти утверждения. Но с каким жаром, я бы сказал, яростью сторонники прежней теории сражались с новыми взглядами! И все потому, что они, якобы, видят вращение Солнца и звезд своими глазами, и для них оно наглядно. С подобной же яростью люди, бывшие свидетелями какого-нибудь события, отстаивают свою версию случившегося, забывая о том, что любой из нас видит вещи по-своему и со своей колокольни. Недаром существует поговорка: «Врет как очевидец».

Из сказанного можно сделать два практических вывода. Первый из них: если теория не может получить доказательств по линии прямой чувственной наглядности, следует продолжать их поиск дальше и дальше, не считаясь со временем. Пока истинность теории не найдет подтверждения, она останется в статусе гипотезы, - не более того. И второе: верификация средствами наглядности может быть достигнута разными способами, а не только непосредственным видением, хотя такая «прямая» верификация была и остается самым надежным и убедительным видом подтверждения правоты выдвигаемых доводов.

ИЕРУСАЛИМ 2018

⁴⁴ John Z. Young. Doubt and Certainty in Science. : A Biologist's Reflections on the Brain. N.Y., Greenwood Press, 1981.
⁴⁵ Бранский В.П. Философское значение проблемы наглядности в современной физике. Москва, URSS, 2010. В: http://www.twirpx.com/file/410038/ (январь 2014)
⁴⁶ В языке есть очень много свидетельств тому, что люди интуитивно понимают под наглядностью. Кроме упомянутых выше примеров, могу сослаться на “Несмотря ни на что…” либо на “Беру не глядя!” при покупке товаров.
⁴⁷ Норберт Винер. Я – математик. Москва – Ижевск, Р & D, 2001, с. 74.
⁴⁸ В: http://ru.wikipedia.org/wiki (февраль 2014).

© А. Соломоник